12.5 Reference Evapotranspiration

One of the most widespread uses of the surface energy balance concept is for determining evapotranspiration. The actual evapotranspiration rate for a given time for a particular location on the land surface can be substantially influenced by site-specific management practices. Thus, often it is useful to estimate the potential or reference evapotranspiration (ET₀) which is the evapotranspiration rate expected for a standard well-watered surface under the prevailing atmospheric conditions. The daily or monthly value of ET₀ can be determined for relatively large regions, and those values can be adjusted to estimate actual ET for a specific location if adequate information is available [8]. Methods for estimating ET₀ or ET commonly are based on the surface energy balance.

12.5.1   Hargreaves Method

One of the simplest approaches for estimating ET₀, the Hargreaves method, was developed to facilitate irrigation management and water planning. The initial work began in California, and the importance of having a simple approach with low data requirements was solidified when the work expanded to Haiti [9]. Building on earlier work in which ET₀ was calculated as a linear function of incoming solar radiation (R_s), Hargreaves found that the product of R_s and air temperature (T) explained much of the variance in measured ET₀. The problem was that measurements of R_s are often unavailable. Therefore, Hargreaves and colleagues developed a way to estimate Rs from knowledge of extraterrestrial radiation (R_a, solar radiation at the top of Earth’s atmosphere for a specific place and time) and air temperature [10].

Since R_a can be accurately estimated based on site latitude and day of year and air temperature measurements are widely available, the Hargreaves method can be used virtually anywhere. The Hargreaves equation is:

(Eq. 12-5)

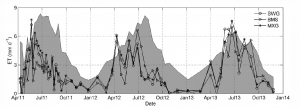
where R_a is the cumulative extraterrestrial radiation for the calculation period converted to units of mm of water, T̄ is the mean temperature (°C) for the calculation period, T_max is mean daily maximum temperature for the calculation period, and T_min is mean daily minimum temperature for the calculation period. This equation is designed for use at 5-day or larger calculation periods and is frequently used with monthly calculation periods. The Hargreaves method is a good choice for ET₀ estimation when the only meteorological data available are air temperatures. For example, the Hargreaves method was used to estimate a 45-yr time series of ET₀ for a large watershed stretching across southwest Oklahoma and part of west Texas, USA (Fig. 12‑7) [11]. Compiling long time series like this would be more difficult, or in some cases impossible, for more data intensive ET₀ estimation methods.

12.5.2   Penman-Monteith Method

A more precise approach was for estimating ET was proposed by Penman, who in 1948 combined the equations for the surface energy balance and for turbulent transport of water vapor away from a saturated evaporating surface [12]. In 1965, Monteith expanded the Penman approach to surfaces where the vapor pressure was less than the saturated vapor pressure (i.e. <100% relative humidity) [13]. The Penman-Monteith equation is:

 (Eq. 12-6)

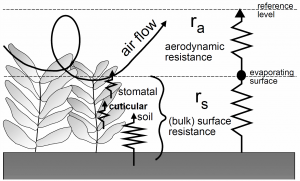
where L is the latent heat of vaporization for water (J kg^-1), R_n is the net radiation (W m^-2), G is the soil heat flux (W m^-2), e_s – e_a is the vapor pressure deficit of the air (kPa), r_a is the density of the air (kg m^-3), c_p is the specific heat capacity of the air at constant pressure (J kg^-1 °C^-1), Δ is the slope of the relationship between saturated vapor pressure and temperature (kPa °C^-1), γ is called the psychrometric constant (kPa °C^-1), r_s is the surface resistance to vapor transport (s m^-1), and r_a is the aerodynamic resistance to vapor transport (s m^-1). These two resistance terms provide a simplified but effective representation of water vapor transport processes near the land surface (Fig. 12‑8).

A panel of experts from the United Nations Food and Agricultural Organization (FAO) has defined the reference surface as, “A hypothetical reference crop with an assumed height of 0.12 m, a fixed surface resistance of 70 s m^-1, and an albedo of 0.23.” [8]. Based on this definition, and employing some approximations for the resistance terms, the FAO Penman-Monteith equation for ET₀ is:

(Eq. 12-7)

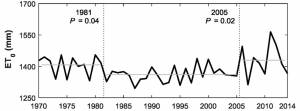
where ET₀ is the reference evapotranspiration (mm d^-1), R_n and G are in MJ m^-2 d^-1, T is the mean daily air temperature at 2-m  height (°C), and u₂ is the mean daily wind speed at 2 m (m s-1). Once ET₀ is determined, site- and day-specific “crop coefficients” (K_c) can be estimated to calculate actual ET from ET₀, i.e. ET = ET₀ × Kc. With judicious use, the FAO Penman-Monteith equation has proven to provide reliable ET₀ estimates for use in crops, grasslands, and forests around the world. For example, the FAO Penman-Monteith equation was used to estimate daily ET₀ during a 3-yr bioenergy crop experiment in Oklahoma (Fig. 12‑9). The results show that actual ET can be substantially less than ET₀ during dry periods (e.g. summers of 2011 and 2012) but can exceed ET₀ during wet periods (e.g. summer of 2013) [14].