12.2 Radiation Basics
The sun, the land, the oceans, and even the atmosphere constantly emit radiation in the form of electromagnetic waves. This radiation can be classified according to its position on the electromagnetic spectrum (Fig. 12‑2). The wavelength of maximum radiation intensity (λmax) emitted by an object is inversely related to the object’s temperature. For a perfect emitter, or blackbody, Wien’s displacement law describes the relationship between λmax and object’s absolute surface temperature, T (K):
![\[ \lambda_m_a_x=\frac{b}{T} \]](https://open.library.okstate.edu/app/uploads/quicklatex/quicklatex.com-341f542ab7b05ab6491ff9977072eeb5_l3.png "Rendered by QuickLaTeX.com")
(Eq. 12-1)
where b = 2,900 μm K.
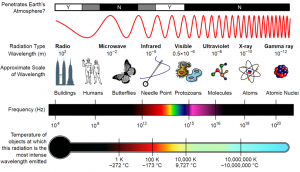
The sun, with a surface temperature of approximately 5,780 K, emits radiation with a peak intensity at wavelength of approximately 0.5 μm, which is in the green range of the visible portion of the electromagnetic spectrum. The Earth’s surface, which has an average temperature of approximately 287 K, emits radiation with a peak intensity of around 10 μm, which is in the infrared portion of the spectrum. Thus, in the context of the surface energy balance, the incoming solar radiation is called shortwave radiation, while the radiation emitted by the land surface and atmosphere is called longwave radiation.
The intensity of radiation emitted by an object depends on the object’s temperature even more strongly than does the wavelength. The equation describing the relationship between an object’s temperature and the intensity of its radiation is called the Stefan-Boltzmann Law which can be written as:
![\[ J_t=\varepsilon \sigma T^4 \]](https://open.library.okstate.edu/app/uploads/quicklatex/quicklatex.com-5855234df204055b09887822a3a3fba8_l3.png "Rendered by QuickLaTeX.com")
(Eq. 12-2)
where Jt is total radiant flux from the emitting surface (W m-2), ε is the emissivity of the surface, σ is the Stefan-Boltzmann constant (5.67 x 10-8 W m-2 K-4), and T is the absolute temperature of the surface (K).
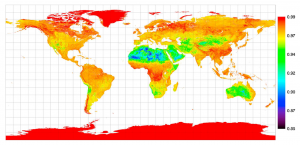
The emissivity is a measure, ranging from 0 to 1, of the effectiveness of a surface in emitting radiation. A perfect emitter has an emissivity of 1. The sun, along with snow and ice covered surfaces are nearly perfect emitters and have emissivity values of approximately 0.99. Water has an emissivity between 0.98 and 0.99, while vegetated surfaces have emissivity values typically ranging from 0.95 to 0.98 for infrared radiation in the 8-13 mm wavelengths [1]. The emissivity of soil is positively related to soil water content [2] and varies between 0.86 and 0.96 [3]. Thus, the composite emissivity of the Earth’s land surface is highest at north and south poles and lowest in the mid-latitude deserts (Fig. 12‑3) [4].
It is important to recognize that just over half of the solar radiation arriving at the top of the Earth’s atmosphere actually arrives at the land surface. On average, about 25% of the incoming solar radiation is reflected back to space by clouds (Fig. 12‑4). An additional 5% is reflected by air molecules, dust, or aerosols in the atmosphere. Approximately 14% of the incoming solar radiation is absorbed by air molecules, dust, or aerosols, and 3% is absorbed by clouds. Only about 31% of the solar radiation travels directly to the Earth’s surface, and an additional 22% reaches the surface as diffuse radiation after being scattered or reflected in the atmosphere.
