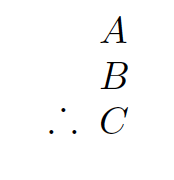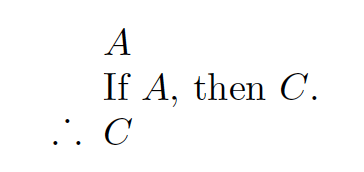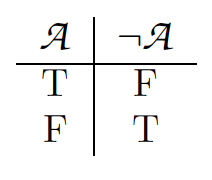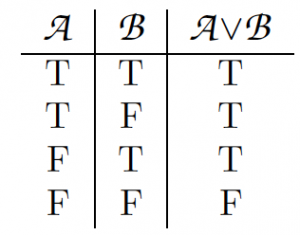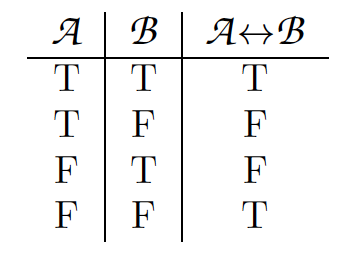4 Sentential Logic
This chapter introduces a logical language called SL. It is a version of sentential logic, because the basic units of the language will represent entire sentences.
I. Sentence letters
In SL, capital letters are used to represent basic sentences. Considered only as a symbol of SL, the letter A could mean any sentence. So when translating from English into SL, it is important to provide a symbolization key. The key provides an English language sentence for each sentence letter used in the symbolization.
For example, consider this argument:
There is an apple on the desk.
If there is an apple on the desk, then Jenny made it to class.
.˙. Jenny made it to class.
This is obviously a valid argument in English. In symbolizing it, we want to preserve the structure of the argument that makes it valid. What happens if we replace each sentence with a letter? Our symbolization key would look like this:
A: There is an apple on the desk.
B: If there is an apple on the desk, then Jenny made it to class.
C: Jenny made it to class.
There is no necessary connection between some sentence A, which could be any sentence, and some other sentences B and C, which could be any sentences. The structure of the argument has been completely lost in this translation.
The important thing about the argument is that the second premise is not merely any sentence, logically divorced from the other sentences in the argument. The second premise contains the first premise and the conclusion as parts. Our symbolization key for the argument only needs to include meanings for A and C, and we can build the second premise from those pieces. So we symbolize the argument this way:
This preserves the structure of the argument that makes it valid, but it still makes use of the English expression ‘If. . . then. . ..’ Although we ultimately want to replace all of the English expressions with logical notation, this is a good start.
The sentences that can be symbolized with sentence letters are called atomic sentences, because they are the basic building blocks out of which more complex sentences can be built. Whatever logical structure a sentence might have is lost when it is translated as an atomic sentence. From the point of view of SL, the sentence is just a letter. It can be used to build more complex sentences, but it cannot be taken apart.
There are only twenty-six letters of the alphabet, but there is no logical limit to the number of atomic sentences. We can use the same letter to symbolize different atomic sentences by adding a subscript, a small number written after the letter. We could have a symbolization key that looks like this:
Keep in mind that each of these is a different sentence letter. When there are subscripts in the symbolization key, it is important to keep track of them.
II. Connectives
Logical connectives are used to build complex sentences from atomic components. There are five logical connectives in SL. This table summarizes them, and they are explained below.
| symbol | what it is called | what it means |
| ¬ | negation | ‘It is not the case that…’ |
| & | conjunction | ‘Both…and…’ |
| ∨ | disjunction | ‘Either…or…” |
| → | conditional | ‘If…then…’ |
| ↔ | biconditional | “…if and only if…’ |
Negation
Consider how we might symbolize these sentences:
- Mary is in Barcelona.
- Mary is not in Barcelona.
- Mary is somewhere besides Barcelona.
In order to symbolize sentence 1, we will need one sentence letter. We can provide a symbolization key:
B: Mary is in Barcelona.
Note that here we are giving B a different interpretation than we did in the previous section. The symbolization key only specifies what B means in a specific context. It is vital that we continue to use this meaning of B so long as we are talking about Mary and Barcelona. Later, when we are symbolizing different sentences, we can write a new symbolization key and use B to mean something else.
Now, sentence 1 is simply B.
Since sentence 2 is obviously related to the sentence 1, we do not want to introduce a different sentence letter. To put it partly in English, the sentence means ‘Not B.’ In order to symbolize this, we need a symbol for logical negation. We will use ‘¬.’ Now we can translate ‘Not B’ to ¬B.
Sentence 3 is about whether or not Mary is in Barcelona, but it does not contain the word ‘not.’ Nevertheless, it is obviously logically equivalent to sentence 2.
They both mean: It is not the case that Mary is in Barcelona. As such, we can translate both sentence 2 and sentence 3 as ¬B.
Consider these further examples:
- The widget can be replaced if it breaks.
- The widget is irreplaceable.
- The widget is not irreplaceable.
If we let R mean ‘The widget is replaceable’, then sentence 4 can be translated as R.
What about sentence 5? Saying the widget is irreplaceable means that it is not the case that the widget is replaceable. So even though sentence 5 is not negative in English, we symbolize it using negation as ¬R.
Sentence 6 can be paraphrased as ‘It is not the case that the widget is irreplaceable.’ Using negation twice, we translate this as ¬¬R. The two negations in a row each work as negations, so the sentence means ‘It is not the case that. . . it is not the case that. . . R.’ If you think about the sentence in English, it is logically equivalent to sentence 4. So when we define logical equivalence in SL, we will make sure that R and ¬¬R are logically equivalent.
More examples:
- Elliott is happy.
- Elliott is unhappy.
If we let H mean ‘Elliot is happy’, then we can symbolize sentence 7 as H.
However, it would be a mistake to symbolize sentence 8 as ¬H. If Elliott is unhappy, then he is not happy— but sentence 8 does not mean the same thing as ‘It is not the case that Elliott is happy.’ It could be that he is not happy but that he is not unhappy either. Perhaps he is somewhere between the two. In order to allow for the possibility that he is indifferent, we would need a new sentence letter to symbolize sentence 8.
For any sentence A: If A is true, then ¬A is false. If ¬A is true, then A is false. Using ‘T’ for true and ‘F’ for false, we can summarize this in a characteristic truth table for negation:
We will discuss truth tables at greater length in the next chapter.
Conjunction
Consider these sentences:
9. Adam is athletic.
10. Barbara is athletic.
11. Adam is athletic, and Barbara is also athletic.
We will need separate sentence letters for 9 and 10, so we define this symbolization key:
A: Adam is athletic.
B: Barbara is athletic.
Sentence 9 can be symbolized as A.
Sentence 10 can be symbolized as B.
Sentence 11 can be paraphrased as ‘A and B.’ In order to fully symbolize this sentence, we need another symbol. We will use ‘ & .’ We translate ‘A and B’ as A & B. The logical connective ‘ & ’ is called CONJUNCTION, and A and B are each called CONJUNCTS.
Notice that we make no attempt to symbolize ‘also’ in sentence 11. Words like ‘both’ and ‘also’ function to draw our attention to the fact that two things are being conjoined. They are not doing any further logical work, so we do not need to represent them in SL.
Some more examples:
12. Barbara is athletic and energetic.
13. Barbara and Adam are both athletic.
14. Although Barbara is energetic, she is not athletic.
15. Barbara is athletic, but Adam is more athletic than she is.
Sentence 12 is obviously a conjunction. The sentence says two things about Barbara, so in English it is permissible to refer to Barbara only once. It might be tempting to try this when translating the argument: Since B means ‘Barbara is athletic’, one might paraphrase the sentences as ‘B and energetic.’ This would be a mistake. Once we translate part of a sentence as B, any further structure is lost. B is an atomic sentence; it is nothing more than true or false. Conversely, ‘energetic’ is not a sentence; on its own it is neither true nor false. We should instead paraphrase the sentence as ‘B and Barbara is energetic.’ Now we need to add a sentence letter to the symbolization key. Let E mean ‘Barbara is energetic.’ Now the sentence can be translated as B & E.
Sentence 13 says one thing about two different subjects. It says of both Barbara and Adam that they are athletic, and in English we use the word ‘athletic’ only once. In translating to SL, it is important to realize that the sentence can be paraphrased as, ‘Barbara is athletic, and Adam is athletic.’ This translates as B & A.
Sentence 14 is a bit more complicated. The word ‘although’ sets up a contrast between the first part of the sentence and the second part. Nevertheless, the sentence says both that Barbara is energetic and that she is not athletic. In order to make each of the conjuncts an atomic sentence, we need to replace ‘she’ with ‘Barbara.’
So we can paraphrase sentence 14 as, ‘Both Barbara is energetic, and Barbara is not athletic.’ The second conjunct contains a negation, so we paraphrase further: ‘Both Barbara is energetic and it is not the case that Barbara is athletic.’ This translates as E & ¬B.
Sentence 15 contains a similar contrastive structure. It is irrelevant for the purpose of translating to SL, so we can paraphrase the sentence as ‘Both Barbara is athletic, and Adam is more athletic than Barbara.’ (Notice that we once again replace the pronoun ‘she’ with her name.) How should we translate the second conjunct? We already have the sentence letter A which is about Adam’s being athletic and B which is about Barbara’s being athletic, but neither is about one of them being more athletic than the other. We need a new sentence letter. Let R mean ‘Adam is more athletic than Barbara.’ Now the sentence translates as B & R.
It is important to keep in mind that the sentence letters A, B, and R are atomic sentences. Considered as symbols of SL, they have no meaning beyond being true or false. We have used them to symbolize different English language sentences that are all about people being athletic, but this similarity is completely lost when we translate to SL. No formal language can capture all the structure of the English language, but as long as this structure is not important to the argument there is nothing lost by leaving it out.
For any sentences A and B, A & B is true if and only if both A and B are true. We can summarize this in the characteristic truth table for conjunction:
Conjunction is symmetrical because we can swap the conjuncts without changing the truth-value of the sentence. Regardless of what A and B are, A & B is logically equivalent to B & A.
Disjunction
Consider these sentences:
16. Either Denison will play golf with me, or he will watch movies.
17. Either Denison or Ellery will play golf with me.
For these sentences we can use this symbolization key:
D: Denison will play golf with me.
E: Ellery will play golf with me.
M: Denison will watch movies.
Sentence 16 is ‘Either D or M .’ To fully symbolize this, we introduce a new symbol. The sentence becomes D ∨ M . The ‘∨’ connective is called DISJUNCTION, and D and M are called DISJUNCTS.
Sentence 17 is only slightly more complicated. There are two subjects, but the English sentence only gives the verb once. In translating, we can paraphrase it as. ‘Either Denison will play golf with me, or Ellery will play golf with me.’ Now it obviously translates as D ∨ E.
Sometimes in English, the word ‘or’ excludes the possibility that both disjuncts are true. This is called an EXCLUSIVE OR. An exclusive or is clearly intended when it says, on a restaurant menu, ‘Entrees come with either soup or salad.’ You may have soup; you may have salad; but, if you want both soup and salad, then you have to pay extra.
At other times, the word ‘or’ allows for the possibility that both disjuncts might be true. This is probably the case with sentence 17, above. I might play with Denison, with Ellery, or with both Denison and Ellery. Sentence 17 merely says that I will play with at least one of them. This is called an INCLUSIVE OR.
The symbol ‘∨’ represents an inclusive or. So D E is true if D is true, if E is true, or if both D and E are true. It is false only if both D and E are false. We can summarize this with the characteristic truth table for disjunction:
Like conjunction, disjunction is symmetrical. A∨B is logically equivalent to B∨A.
These sentences are somewhat more complicated:
18. Either you will not have soup, or you will not have salad.
19. You will have neither soup nor salad.
20. You get either soup or salad, but not both.
We let S1 mean that you get soup and S2 mean that you get salad.
Sentence 18 can be paraphrased in this way: ‘Either it is not the case that you get soup, or it is not the case that you get salad.’ Translating this requires both disjunction and negation. It becomes ¬S1 ∨ ¬S2.
Sentence 19 also requires negation. It can be paraphrased as, ‘It is not the case that either that you get soup or that you get salad.’ We need some way of indicating that the negation does not just negate the right or left disjunct, but rather negates the entire disjunction. In order to do this, we put parentheses around the disjunction: ‘It is not the case that (S1 ∨ S2).’ This becomes simply ¬(S1 ∨ S2). Notice that the parentheses are doing important work here. The sentence ¬S1 ∨ S2 would mean ‘Either you will not have soup, or you will have salad.’
Sentence 20 is an exclusive or. We can break the sentence into two parts. The first part says that you get one or the other. We translate this as (S1 ∨ S2). The second part says that you do not get both. We can paraphrase this as, ‘It is not the case both that you get soup and that you get salad.’ Using both negation and conjunction, we translate this as ¬(S1 & S2). Now we just need to put the two parts together. As we saw above, ‘but’ can usually be translated as a conjunction. Sentence 20 can thus be translated as (S1 ∨ S2) & ¬(S1 & S2).
Although ‘∨’ is an inclusive or, we can symbolize an exclusive or in SL. We just need more than one connective to do it.
Conditional
For the following sentences, let R mean ‘You will cut the red wire’ and B mean ‘The bomb will explode.’
21. If you cut the red wire, then the bomb will explode.
22. The bomb will explode only if you cut the red wire.
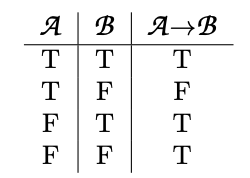
Sentence 21 can be translated partially as ‘If R, then B.’ We will use the symbol ‘→’ to represent logical entailment. The sentence becomes R → B. The connective is called a CONDITIONAL. The sentence on the left-hand side of the conditional (R in this example) is called the ANTECEDENT. The sentence on the right-hand side (B) is called the CONSEQUENT.
Sentence 22 is also a conditional. Since the word ‘if’ appears in the second half of the sentence, it might be tempting to symbolize this in the same way as sentence 21. That would be a mistake.
The conditional R → B says that if R were true, then B would also be true. It does not say that your cutting the red wire is the only way that the bomb could explode. Someone else might cut the wire, or the bomb might be on a timer. The sentence R → B does not say anything about what to expect if R is false. Sentence 22 is different. It says that the only conditions under which the bomb will explode involve your having cut the red wire; i.e., if the bomb explodes, then you must have cut the wire. As such, sentence 22 should be symbolized as B → R.
It is important to remember that the connective ‘→’ says only that, if the antecedent is true, then the consequent is true. It says nothing about the causal connection between the two events. Translating sentence 22 as B → R does not mean that the bomb exploding would somehow have caused your cutting the wire. Both sentence 21 and 22 suggest that, if you cut the red wire, your cutting the red wire would be the cause of the bomb exploding. They differ on the logical connection. If sentence 22 were true, then an explosion would tell us— those of us safely away from the bomb— that you had cut the red wire. Without an explosion, sentence 22 tells us nothing.
The conditional is asymmetrical. You cannot swap the antecedent and consequent without changing the meaning of the sentence, because A→B and B→A are not logically equivalent.
Not all sentences of the form ‘If. . . then. . .’ are conditionals. Consider this sentence:
23. If anyone wants to see me, then I will be on the porch.
If I say this, it means that I will be on the porch, regardless of whether anyone wants to see me or not— but if someone did want to see me, then they should look for me there. If we let P mean ‘I will be on the porch,’ then sentence 23 can be translated simply as P .
Biconditional
Consider these sentences:
24. The figure on the board is a triangle only if it has exactly three sides.
25. The figure on the board is a triangle if it has exactly three sides.
26. The figure on the board is a triangle if and only if it has exactly three sides.
Let T mean ‘The figure is a triangle’ and S mean ‘The figure has three sides.’
Sentence 24, for reasons discussed above, can be translated as T → S.
Sentence 25 is importantly different. It can be paraphrased as, ‘If the figure has three sides, then it is a triangle.’ So it can be translated as S → T .
Sentence 26 says that T is true if and only if S is true; we can infer S from T , and we can infer T from S. This is called a biconditional, because it entails the two conditionals S → T and T → S. We will use ‘↔’ to represent the biconditional; sentence 26 can be translated as S ↔ T .
We could abide without a new symbol for the biconditional. Since sentence 26 means ‘T → S and S → T ,’ we could translate it as (T → S) & (S → T ). We would need parentheses to indicate that (T → S) and (S → T ) are separate conjuncts; the expression T → S & S → T would be ambiguous.
Because we could always write (A → B) & (B → A) instead of A ↔ B, we do not strictly speaking need to introduce a new symbol for the biconditional. Nevertheless, logical languages usually have such a symbol. SL will have one, which makes it easier to translate phrases like ‘if and only if.
A ↔ B is true if and only if A and B have the same truth value. This is the characteristic truth table for the biconditional:
III. Other symbolization
We have now introduced all of the connectives of SL. We can use them together to translate many kinds of sentences. Consider these examples of sentences that use the English-language connective ‘unless’:
27. Unless you wear a jacket, you will catch cold.
28. You will catch cold unless you wear a jacket.
Let J mean ‘You will wear a jacket’ and let D mean ‘You will catch a cold.’
We can paraphrase sentence 27 as ‘Unless J , D.’ This means that if you do not wear a jacket, then you will catch cold; with this in mind, we might translate it as ¬J → D. It also means that if you do not catch a cold, then you must have worn a jacket; with this in mind, we might translate it as ¬D → J .
Which of these is the correct translation of sentence 27? Both translations are correct, because the two translations are logically equivalent in SL.
Sentence 28, in English, is logically equivalent to sentence 27. It can be translated as either ¬J → D or ¬D → J .
When symbolizing sentences like sentence 27 and sentence 28, it is easy to get turned around. Since the conditional is not symmetric, it would be wrong to translate either sentence as J →¬D. Fortunately, there are other logically equivalent expressions. Both sentences mean that you will wear a jacket or— if you do not wear a jacket— then you will catch a cold. So we can translate them as J ∨ D. (You might worry that the ‘or’ here should be an exclusive or. However, the sentences do not exclude the possibility that you might both wear a jacket and catch a cold; jackets do not protect you from all the possible ways that you might catch a cold.)
IV. Sentences of SL
The sentence ‘Apples are red, or berries are blue’ is a sentence of English, and the sentence ‘(A ∨ B)’ is a sentence of SL. Although we can identify sentences of English when we encounter them, we do not have a formal definition of ‘sentence of English’. In SL, it is possible to formally define what counts as a sentence. This is one respect in which a formal language like SL is more precise than a natural language like English.
It is important to distinguish between the logical language SL, which we are developing, and the language that we use to talk about SL. When we talk about a language, the language that we are talking about is called the object language. The language that we use to talk about the OBJECT LANGUAGE is called the METALANGUAGE.
The object language in this chapter is SL. The metalanguage is English— not conversational English, but English supplemented with some logical and mathematical vocabulary. The sentence ‘(A ∨ B)’ is a sentence in the object language, because it uses only symbols of SL. The word ‘sentence’ is not itself part of SL, however, so the sentence ‘This expression is a sentence of SL’ is not a sentence of SL. It is a sentence in the metalanguage, a sentence that we use to talk about SL.
In this section, we will give a formal definition for ‘sentence of SL.’ The definition itself will be given in mathematical English, the metalanguage.
Expressions
There are three kinds of symbols in SL:
| sentences letters with subscripts, as needed | A, B, C,…,Z or as needed: A1, B1, Z1, A2, A25, J375,… |
| connectives | ¬, &, ∨, →, ↔ |
| parentheses | ( , ) |
We define an EXPRESSION of SL as any string of symbols of SL. Take any of the symbols of SL and write them down, in any order, and you have an expression.
Well-formed formulae
Since any sequence of symbols is an expression, many expressions of SL will be gobbledegook. A meaningful expression is called a well-formed formula. It is common to use the acronym wff ; the plural is wffs.
Obviously, individual sentence letters like A and G13 will be wffs. We can form further wffs out of these by using the various connectives. Using negation, we can get ¬A and ¬G13. Using conjunction, we can get A & G13, G13 & A, A & A, and G13 & G13. We could also apply negation repeatedly to get wffs ¬¬A or apply negation along with conjunction to get wffs like ¬(A & G13) and (G13 & G13). The possible combinations are endless, even starting with just these two sentence letters, and there are infinitely many sentence letters. So there is no point in trying to list all the wffs.
Instead, we will describe the process by which wffs can be constructed. Consider negation: Given any wff A of SL, A is a wff of SL. It is important here that A is not the sentence letter A. Rather, it is a variable that stands in for any wff at all. Notice that this variable A is not a symbol of SL, so A is not an expression of SL. Instead, it is an expression of the metalanguage that allows us to talk about infinitely many expressions of SL: all of the expressions that start with the negation symbol. Because A is part of the metalanguage, it is called a metavariable.We can say similar things for each of the other connectives. For instance, if A and B are wffs of SL, then (A & B) is a wff of SL. Providing clauses like this for all of the connectives, we arrive at the following formal definition for a well-formed formula of SL:
1. Every atomic sentence is a wff.
2. If A is a wff, then ¬A is a wff of SL.
3. If A and B are wffs, then (A & B) is a wff.
4. If A and B are wffs, then (A ∨ B) is a wff.
5. If A and B are wffs, then (A → B) is a wff.
6. If A and B are wffs, then (A ↔ B) is a wff.
7. All and only wffs of SL can be generated by applications of these rules.
Notice that we cannot immediately apply this definition to see whether an arbitrary expression is a wff. Suppose we want to know whether or not D is a wff of SL. Looking at the second clause of the definition, we know that¬¬¬D is a wff if ¬¬D is a wff. So now we need to ask whether or not ¬¬D is a wff. Again looking at the second clause of the definition, D is a wff if D is. Again, D is a wff if D is a wff. Now D is a sentence letter, an atomic sentence of SL, so we know that D is a wff by the first clause of the definition. So for a compound formula like D, we must apply the definition repeatedly. Eventually we arrive at the atomic sentences from which the wff is built up.
Definitions like this are called recursive. Recursive definitions begin with some specifiable base elements and define ways to indefinitely compound the base elements. Just as the recursive definition allows complex sentences to be built up from simple parts, you can use it to decompose sentences into their simpler parts. To determine whether or not something meets the definition, you may have to refer back to the definition many times.
The connective that you look to first in decomposing a sentence is called the MAIN LOGICAL OPERATOR of that sentence. For example: The main logical operator of ¬(E ∨ (F → G)) is negation, ¬. The main logical operator of (¬E ∨ (F → G)) is disjunction, ∨.
Sentences
Recall that a sentence is a meaningful expression that can be true or false. Since the meaningful expressions of SL are the wffs and since every wff of SL is either true or false, the definition for a sentence of SL is the same as the definition for a wff. Not every formal language will have this nice feature. In the language QL, which is developed later in the book, there are wffs which are not sentences.
The recursive structure of sentences in SL will be important when we consider the circumstances under which a particular sentence would be true or false. The sentence D is true if and only if the sentence D is false, and so on through the structure of the sentence until we arrive at the atomic components: ¬¬¬D is true if and only if the atomic sentence D is false. We will return to this point in the next chapter.
Notational conventions
A wff like (Q & R) must be surrounded by parentheses, because we might apply the definition again to use this as part of a more complicated sentence. If we negate (Q & R), we get (Q & R). If we just had Q & R without the parentheses and put a negation in front of it, we would have Q & R. It is most natural to read this as meaning the same thing as ( Q & R), something very different than (Q & R). The sentence (Q & R) means that it is not the case that both Q and R are true; Q might be false or R might be false, but the sentence does not tell us which. The sentence (¬Q & R) means specifically that Q is false and that R is true. As such, parentheses are crucial to the meaning of the sentence.
So, strictly speaking, Q & R without parentheses is not a sentence of SL. When using SL, however, we will often be able to relax the precise definition so as to make things easier for ourselves. We will do this in several ways.
First, we understand that Q & R means the same thing as (Q & R). As a matter of convention, we can leave off parentheses that occur around the entire sentence.
Second, it can sometimes be confusing to look at long sentences with many, nested pairs of parentheses. We adopt the convention of using square brackets ‘[’ and ‘]’ in place of parenthesis. There is no logical difference between (P ∨ Q) and [P ∨ Q], for example. The unwieldy sentence (((H → I) ∨ (I → H)) & (J ∨ K)) could be written in this way: [(H → I) ∨ (I → H)] & (J ∨ K).
Third, we will sometimes want to translate the conjunction of three or more sentences. For the sentence ‘Alice, Bob, and Candice all went to the party’, suppose we let A mean ‘Alice went’, B mean ‘Bob went’, and C mean ‘Candice went.’ The definition only allows us to form a conjunction out of two sentences, so we can translate it as (A & B) & C or as A & (B & C). There is no reason to distinguish between these, since the two translations are logically equivalent. There is no logical difference between the first, in which (A & B) is conjoined with C, and the second, in which A is conjoined with (B & C). So we might as well just write A & B & C. As a matter of convention, we can leave out parentheses when we conjoin three or more sentences.
Fourth, a similar situation arises with multiple disjunctions. ‘Either Alice, Bob, or Candice went to the party’ can be translated as (A ∨ B) ∨ C or as A ∨(B ∨ C). Since these two translations are logically equivalent, we may write A ∨ B ∨ C.
These latter two conventions only apply to multiple conjunctions or multiple disjunctions. If a series of connectives includes both disjunctions and conjunctions, then the parentheses are essential; as with (A & B) C and A & (B C). The parentheses are also required if there is a series of conditionals or biconditionals; as with (A → B) → C and A ↔ (B ↔ C).
We have adopted these four rules as notational conventions, not as changes to the definition of a sentence. Strictly speaking, A B C is still not a sentence. Instead, it is a kind of shorthand. We write it for the sake of convenience, but we really mean the sentence (A ∨ (B ∨ C)).
If we had given a different definition for a wff, then these could count as wffs. We might have written rule 3 in this way: “If A, B, . . . Z are wffs, then (A & B & . . . & Z), is a wff.” This would make it easier to translate some English sentences, but would have the cost of making our formal language more complicated. We would have to keep the complex definition in mind when we develop truth tables and a proof system. We want a logical language that is expressively simple and allows us to translate easily from English, but we also want a formally simple language. Adopting notational conventions is a compromise between these two desires.
V. Practice Exercises
* Part A Using the symbolization key given, translate each English-language sentence into SL.
M: Those creatures are men in suits.
C: Those creatures are chimpanzees.
G: Those creatures are gorillas.
- Those creatures are not men in suits.
- Those creatures are men in suits, or they are not.
- Those creatures are either gorillas or chimpanzees.
- Those creatures are neither gorillas nor chimpanzees.
- If those creatures are chimpanzees, then they are neither gorillas nor men in suits.
- Unless those creatures are men in suits, they are either chimpanzees or they are gorillas.
Part B Using the symbolization key given, translate each English-language sentence into SL.
A: Mister Ace was murdered.
B: The butler did it.
C: The cook did it.
D: The Duchess is lying.
E: Mister Edge was murdered.
F: The murder weapon was a frying pan.
- Either Mister Ace or Mister Edge was murdered.
- If Mister Ace was murdered, then the cook did it.
- If Mister Edge was murdered, then the cook did not do it.
- Either the butler did it, or the Duchess is lying.
- The cook did it only if the Duchess is lying.
- If the murder weapon was a frying pan, then the culprit must have been the cook.
- If the murder weapon was not a frying pan, then the culprit was either the cook or the butler.
- Mister Ace was murdered if and only if Mister Edge was not murdered.
- The Duchess is lying, unless it was Mister Edge who was murdered.
- If Mister Ace was murdered, he was done in with a frying pan.
- Since the cook did it, the butler did not.
- Of course the Duchess is lying!
* Part C Using the symbolization key given, translate each English-language sentence into SL.
E1: Ava is an electrician.
E2: Harrison is an electrician.
F1: Ava is a firefighter.
F2: Harrison is a firefighter.
S1: Ava is satisfied with her career.
S2: Harrison is satisfied with his career.
- Ava and Harrison are both electricians.
- If Ava is a firefighter, then she is satisfied with her career.
- Ava is a firefighter, unless she is an electrician.
- Harrison is an unsatisfied electrician.
- Neither Ava nor Harrison is an electrician.
- Both Ava and Harrison are electricians, but neither of them find it satisfying.
- Harrison is satisfied only if he is a firefighter.
- If Ava is not an electrician, then neither is Harrison, but if she is, then he is too.
- Ava is satisfied with her career if and only if Harrison is not satisfied with his.
- If Harrison is both an electrician and a firefighter, then he must be satisfied with his work.
- It cannot be that Harrison is both an electrician and a firefighter.
- Harrison and Ava are both firefighters if and only if neither of them is an electrician.
* Part D Give a symbolization key and symbolize the following sentences in SL.
- Alice and Bob are both spies.
- If either Alice or Bob is a spy, then the code has been broken.
- If neither Alice nor Bob is a spy, then the code remains unbroken.
- The German embassy will be in an uproar, unless someone has broken the code.
- Either the code has been broken or it has not, but the German embassy will be in an uproar regardless.
- Either Alice or Bob is a spy, but not both.
Part E Give a symbolization key and symbolize the following sentences in SL.
- If Gregor plays first base, then the team will lose.
- The team will lose unless there is a miracle.
- The team will either lose or it won’t, but Gregor will play first base regardless.
- Gregor’s mom will bake cookies if and only if Gregor plays first base.
- If there is a miracle, then Gregor’s mom will not bake cookies.
Part F For each argument, write a symbolization key and translate the argument as well as possible into SL.
- If Dorothy plays the piano in the morning, then Roger wakes up cranky. Dorothy plays piano in the morning unless she is distracted. So if Roger does not wake up cranky, then Dorothy must be distracted.
- It will either rain or snow on Tuesday. If it rains, Neville will be sad. If it snows, Neville will be cold. Therefore, Neville will either be sad or cold on Tuesday.
- If Zoog remembered to do his chores, then things are clean but not neat. If he forgot, then things are neat but not clean. Therefore, things are either neat or clean— but not both.
* Part G For each of the following: (a) Is it a wff of SL? (b) Is it a sentence of SL, allowing for notational conventions?
- (A)
- J374 ∨ ¬J374
- ¬¬¬¬F
- ¬ & S
- (G & ¬G)
- A → A
- (A → (A & ¬F )) ∨ (D ↔ E)
- [(Z ↔ S) → W ] & [J ∨ X]
- (F ↔ ¬D → J ) ∨ (C & D)
Part H
- 1. Are there any wffs of SL that contain no sentence letters? Why or why not?
- 2. In the chapter, we symbolized an exclusive or using ∨, & , and ¬. How could you translate an exclusive or using only two connectives? Is there any way to translate an exclusive or using only one connective?