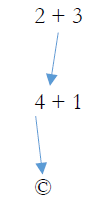If we want to study how we ought to reason (normative) we should start by looking at the primary way that we do reason (descriptive): through the use of arguments. In order to develop a theory of good reasoning, we will start with an account of what an argument is and then proceed to talk about what constitutes a “good” argument.

I. Arguments

• Arguments are a set of statements (premises and conclusion).
• The premises provide evidence, reasons, and grounds for the conclusion.
• The conclusion is what is being argued for.
• An argument attempts to draw some logical connection between the premises and the conclusion.
• And in doing so, the argument expresses an inference: a process of reasoning from the truth of the premises to the truth of the conclusion.

In this instance, the conclusion is the first sentence (“The world will end…”); the premises (however dubious) are revealed in the second sentence (“I know this because…”).

II. Statements

Conclusions and premises are articulated in the form of statements. Statements are sentences that can be determined to possess or lack truth. Some examples of true-or-false statements can be found below. (Notice that while some statements are categorically true or false, others may or may not be true depending on when they are made or who is making them.)

Examples of sentences that are statements:

1. It is below 40°F outside.
2. Oklahoma is north of Texas.
3. The Denver Broncos will make it to the Super Bowl.
4. Russell Westbrook is the best point guard in the league.
5. I like broccoli.
6. I shouldn’t eat French fries.
7. Time travel is possible.
8. If time travel is possible, then you can be your own father or mother.

However, there are many sentences that cannot so easily be determined to be true or false. For this reason, these sentences identified below are not considered statements.

1. Questions: “What time is it?”
2. Commands: “Do your homework.”
3. Requests: “Please clean the kitchen.”
4. Proposals: “Let’s go to the museum tomorrow.”

Question: Why are arguments only made up of statements?

First, we only believe statements. It doesn’t make sense to talk about believing questions, commands, requests or proposals. Contrast sentences on the left that are not statements with sentences on the right that are statements:

It would be non-sensical to say that we believe the non-statements (e.g. “I believe what time is it?”). But it makes perfect sense to say that we believe the statements (e.g. “I believe the time is 11 a.m.”). If conclusions are the statements being argued for, then they are also ideas we are being persuaded to believe. Therefore, only statements can be conclusions.

Second, only statements can provide reasons to believe.

• Q: Why should I believe that it is 11:00 a.m.? A: Because the clock says it is 11a.m.
• Q: Why should I believe that we are going to the museum tomorrow? A: Because today we are making plans to go.

Sentences that cannot be true or false cannot provide reasons to believe. So, if premises are meant to provide reasons to believe, then only statements can be premises.

III. Representing Arguments

As we concern ourselves with arguments, we will want to represent our arguments in some way, indicating which statements are the premises and which statement is the conclusion. We shall represent arguments in two ways. For both ways, we will number the premises.

In order to identify the conclusion, we will either label the conclusion with a (c) or (conclusion). Or we will mark the conclusion with the ∴ symbol

Example Argument:

There will be a war in the next year. I know this because there has been a massive buildup in weapons. And every time there is a massive buildup in weapons, there is a war. My guru said the world will end on August 6, 2045.

• There has been a massive buildup in weapons.
• Every time there has been a massive buildup in weapons, there is a war.

(c) There will be a war in the next year.

Or

• There has been a massive buildup in weapons.
• Every time there has been a massive buildup in weapons, there is a war.

∴ There will be a war in the next year.

Of course, arguments do not come labeled as such. And so we must be able to look at a passage and identify whether the passage contains an argument and if it does, we should also be identify which statements are the premises and which statement is the conclusion. This is harder than you might think!

Example:

There is no argument here. There is no statement being argued for. There are no statements being used as reasons to believe. This is simply a report of information.

The following are also not arguments:

Advice: Be good to your friends; your friends will be good to you.

Warnings: No lifeguard on duty. Be careful.

Associated claims: Fear leads to anger. Anger leads to the dark side.

When you have an argument, the passage will express some process of reasoning. There will be statements presented that serve to help the speaker building a case for the conclusion.

IV. How to Look for Arguments^[1]

How do we identify arguments in real life? There are no easy, mechanical rules, and we usually have to rely on the context in order to determine which are the premises and the conclusions. But sometimes the job can be made easier by the presence of certain premise or conclusion indicators. For example, if a person makes a statement, and then adds “this is because …,” then it is quite likely that the first statement is presented as a conclusion, supported by the statements that come afterward. Other words in English that might be used to indicate the premises to follow include:

• since
• firstly, secondly, …
• for, as, after all
• assuming that, in view of the fact that
• follows from, as shown / indicated by
• may be inferred / deduced / derived from

Of course whether such words are used to indicate premises or not depends on the context. For example, “since” has a very different function in a statement like “I have been here since noon,” unlike “X is an even number since X is divisible by 4.” In the first instance (“since noon”) “since” means “from.” In the second instance, “since” means “because.”

Conclusions, on the other hand, are often preceded by words like:

• therefore, so, it follows that
• hence, consequently
• suggests / proves / demonstrates that
• entails, implies

Here are some examples of passages that do not contain arguments.

1. When people sweat a lot they tend to drink more water. [Just a single statement, not enough to make an argument.]

2. Once upon a time there was a prince and a princess. They lived happily together and one day they decided to have a baby. But the baby grew up to be a nasty and cruel person and they regret it very much. [A chronological description of facts composed of statements but no premise or conclusion.]

3. Can you come to the meeting tomorrow? [A question that does not contain an argument.]

Exercises

Do these passages contain arguments? If so, what are their conclusions?

1. Cutting the interest rate will have no effect on the stock market this time around, as people have been expecting a rate cut all along. This factor has already been reflected in the market.
2. So it is raining heavily and this building might collapse. But I don’t really care.
3. Virgin would then dominate the rail system. Is that something the government should worry about? Not necessarily. The industry is regulated, and one powerful company might at least offer a more coherent schedule of services than the present arrangement has produced. The reason the industry was broken up into more than 100 companies at privatization was not operational, but political: the Conservative government thought it would thus be harder to renationalize (The Economist 12/16/2000).
4. Bill will pay the ransom. After all, he loves his wife and children and would do everything to save them.
5. All of Russia’s problems of human rights and democracy come back to three things: the legislature, the executive and the judiciary. None works as well as it should. Parliament passes laws in a hurry, and has neither the ability nor the will to call high officials to account. State officials abuse human rights (either on their own, or on orders from on high) and work with remarkable slowness and disorganization. The courts almost completely fail in their role as the ultimate safeguard of freedom and order (The Economist 11/25/2000).
6. Most mornings, Park Chang Woo arrives at a train station in central Seoul, South Korea’s capital. But he is not commuter. He is unemployed and goes there to kill time. Around him, dozens of jobless people pass their days drinking soju, a local version of vodka. For the moment, middle-aged Mr. Park would rather read a newspaper. He used to be a bricklayer for a small construction company in Pusan, a southern port city. But three years ago the country’s financial crisis cost him that job, so he came to Seoul, leaving his wife and two children behind. Still looking for work, he has little hope of going home any time soon (The Economist 11/25/2000).
7. For a long time, astronomers suspected that Europa, one of Jupiter’s many moons, might harbour a watery ocean beneath its ice-covered surface. They were right. Now the technique used earlier this year to demonstrate the existence of the Europan ocean has been employed to detect an ocean on another Jovian satellite, Ganymede, according to work announced at the recent American Geo-physical Union meeting in San Francisco (The Economist 12/16/2000).
8. There are no hard numbers, but the evidence from Asia’s expatriate community is unequivocal. Three years after its handover from Britain to China, Hong Kong is unlearning English. The city’s gweilos (Cantonese for “ghost men”) must go to ever greater lengths to catch the oldest taxi driver available to maximize their chances of comprehension. Hotel managers are complaining that they can no longer find enough English-speakers to act as receptionists. Departing tourists, polled at the airport, voice growing frustration at not being understood (The Economist 1/20/2001).

V. Evaluating Arguments

Q: What does it mean for an argument to be good? What are the different ways in which arguments can be good? Good arguments:

1. Are persuasive.
2. Have premises that provide good evidence for the conclusion.
3. Contain premises that are true.
4. Reach a true conclusion.
5. Provide the audience good reasons for accepting the conclusion.

The focus of logic is primarily about one type of goodness: The logical relationship between premises and conclusion.

An argument is good in this sense if the premises provide good evidence for the conclusion. But what does it mean for premises to provide good evidence? We need some new concepts to capture this idea of premises providing good logical support. In order to do so, we will first need to distinguish between two types of argument.

VI. Two Types of Arguments

The two main types of arguments are called deductive and inductive arguments. We differentiate them in terms of the type of support that the premises are meant to provide for the conclusion.

Deductive Arguments are arguments in which the premises are meant to provide conclusive logical support for the conclusion.

Examples:

#1:

1. All humans are mortal

2. Socrates is a human.

∴ Therefore, Socrates is mortal.

#2:

1. No student in this class will fail.

2. Mary is a student in this class.

∴ Therefore, Mary will not fail.

#3:

1. A intersects lines B and C.

2. Lines A and B form a 90-degree angle

3. Lines A and C form a 90-degree angle.

∴ B and C are parallel lines.

Inductive arguments are, by their very nature, risky arguments.

Arguments in which premises provide probable support for the conclusion.

Statistical Examples:

#1:

1. Ten percent of all customers in this restaurant order soda.

2. John is a customer.

∴ John will not order Soda..

#2:

1. Some students work on campus.

2. Bill is a student.

∴ Bill works on campus.

#3:

1. Vegas has the Carolina Panthers as a six-point favorite for the super bowl.

∴ Carolina will win the Super Bowl.

VII. Good Deductive Arguments

The First Type of Goodness: Premises play their function – they provide conclusive logical support.

Deductive and inductive arguments have different aims. Deductive argument attempt to provide conclusive support or reasons; inductive argument attempt to provide probable reasons or support. So we must evaluate these two types of arguments.

Deductive arguments attempt to be valid.

To put validity in another way: if the premises are true, then the conclusion must be true.

It is very important to note that validity has nothing to do with whether or not the premises are, in fact, true and whether or not the conclusion is in fact true; it merely has to do with a certain conditional claim. If the premises are true, then the conclusion must be true.

Q: What does this mean?

• The validity of an argument does not depend upon the actual world. Rather, it depends upon the world described by the premises.
• First, consider the world described by the premises. In this world, is it logically possible for the conclusion to be false? That is, can you even imagine a world in which the conclusion is false?

Reflection Questions:

1. Can you have a valid argument with false premises?
   • If you cannot, then why not?
   • If you can, then provide an example of a valid argument.
2. Can you have a valid argument with a false conclusion?
   • If you cannot, then why not?
   • If you can, then provide an example of a valid argument.

You should convince yourself that validity is not just about the actual truth or falsity of the premises and conclusion. Rather, validity only has to do with a certain logical relationship between the truth of the premise and the truth of the conclusion. So the only possible combination that is ruled out by a valid argument is a set of true premises and false conclusion.

Let’s go back to example #1. Here are the premises:

1. All humans are mortal.

2. Socrates is a human.

If both of these premises are true, then every human that we find must be a mortal. And this means, that it must be the case that if Socrates is a human, that Socrates is mortal.

Reflection Questions about Invalid Arguments:

1. Can you have an invalid argument with a true premise?
2. Can you have an invalid argument with true premises and a true conclusion?

The second type of goodness for deductive arguments: The premises provide us the right reasons to accept the conclusion.

Soundness Versus Validity:

Our original argument is a sound one:

1. All humans are mortal.

2. Socrates is a human.

∴ Socrates is mortal.

Question: Can a sound argument have a false conclusion?

VIII. From Deductive Arguments to Inductive Arguments

Question: What happens if we mix around the premises and conclusion?

1. All humans are mortal.

2. Socrates is mortal.

∴ Socrates is a human.

1. Socrates is mortal

2. Socrates is a human.

∴ All humans are mortal.

Are these valid deductive arguments?

NO, but they are common inductive arguments.

Other examples:

Suppose that there are two opaque glass jars with different color marbles in them.

1. All the marbles in jar #1 are blue.

2. This marble is blue.

∴ This marble came from jar #1.

1. This marble came from jar #2.

2. This marble is red.

∴ All the marbles in jar #2 are red.

While this is a very risky argument, what if we drew 100 marbles from jar #2 and found that they were all red? Would this affect the second argument’s validity?

IX. Inductive Arguments:

The aim of an inductive argument is different from the aim of deductive argument because the type of reasons we are trying to provide are different. Therefore, the function of the premises is different in deductive and inductive arguments. And again, we can split up goodness into two types when considering inductive arguments:

1. The premises provide the right logical support.
2. The premises provide the right type of reason.

Logical Support:

Remember that for inductive arguments, the premises are intended to provide probable support for the conclusion. Thus, we shall begin by discussing a fairly rough, coarse-grained way of talking about probable support by introducing the notions of strong and weak inductive arguments.

A strong inductive argument:

1. 1. The vast majority of Europeans speak at least two languages.
   2. Sam is a European.

∴ Sam speaks two languages.

Weak inductive argument:

1. 1. This quarter is a fair coin.

∴ Therefore, the next coin flip will land heads.

Weak inductive argument:

1. 1. At least one dog in this town has rabies.
   2. Fido is a dog that lives in this town.

∴ Fido has rabies.

The Right Type of Reasons. As we noted above, the right type of reasons are true statements. So what happens when we get an inductive argument that is good in the first sense (right type of logical support) and good in the second sense (the right type of reasons)? Corresponding to the notion of soundness for deductive arguments, we call inductive arguments that are good in both senses cogent arguments.

• With which of the following types of premises and conclusions can you have a strong inductive argument?
• With which of the following types of premises and conclusions can you have a cogent inductive argument?

X. Steps for Evaluating Arguments:

1. Read a passage and assess whether or not it contains an argument.
2. If it does contain an argument, then identify the conclusion and premises.
3. Is this a valid deductive argument?
   • If yes, then assess it for soundness.
   • If not, then treat it as an inductive argument (step 3).
4. Is the inductive argument strong or weak?
   • If the inductive argument is strong, then is it cogent?

XI. Evaluating Real–World Arguments

An important part of evaluating arguments is not to represent the arguments of others in a deliberately weak way.

For example, suppose that I state the following:

All humans are mortal, so Socrates is mortal.

Is this valid? Not as it stands. But clearly, I believe that Socrates is a human being. Or I thought that was assumed in the conversation. That premise was clearly an implicit one.

So one of the things we can do in the evaluation of argument is to take an argument as it is stated, and represent it in a way such that it is a valid deductive argument or a strong inductive one. In doing so, we are making explicit what one would have to assume to provide a good argument (in the sense that the premises provide good – conclusive or probable – reason to accept the conclusion).

Example 1:

The teacher’s policy on extra credit was unfair because Sally was the only person to have a chance at receiving extra credit.

1. Sally was the only person to have a chance at receiving extra credit.
2. The teacher’s policy on extra credit is fair only if everyone gets a chance to receive extra credit.

Therefore, the teacher’s policy on extra credit was unfair.

Valid argument

Example 2:

Sally didn’t train very hard so she didn’t win the race.

Valid:

1. Sally didn’t train very hard.
2. If you don’t train hard, you won’t win the race.

Therefore, Sally didn’t win the race.

Strong (not valid):

1. Sally didn’t train very hard.
2. If you won the race, you trained hard.

Therefore, Sally didn’t win the race.

Strong:

1. Sally didn’t train very hard.
2. Those who don’t train hard are likely not to win.

Therefore, Sally didn’t win.

Example 3:

Ordinary workers receive worker’s compensation benefits if they suffer an on-the-job injury. However, universities have no obligations to pay similar compensation to student athletes if they are hurt while playing sports. So, universities are not doing what they should.

1. Ordinary workers receive worker’s compensation benefits if they suffer an on-the-job injury that prevents them working.
2. Student athletes are just like ordinary workers except that their job is to play sports.
3. So if student athletes are injured while playing sports, they should also be provided worker’s compensation benefits.
4. Universities have no obligations to provide injured student athletes compensation.

Therefore, universities are not doing what they should.

Deductively valid argument

Example 4:

If Obama couldn’t implement a single-payer healthcare system in his first term as president, then the next president will not be able to implement a single-payer healthcare system.

1. Obama couldn’t implement a single-payer healthcare system.
2. In Obama’s first term as president, both the House and Senate were under Democratic control.
3. The next president will either be dealing with the Republican-controlled house and senate or at best, a split legislature.
4. Obama’s first term as president will be much easier than the next president’s term in terms of passing legislation.

Therefore, the next president will not be able to implement a single-payer healthcare system.

Strong inductive argument

Example 5:

Sam is weaker than John. Sam is slower than John. So Sam’s time on the obstacle will be slower than John’s.

1. Sam is weaker than John.
2. Sam is slower than John.
3. A person’s strength and speed inversely correlate with their time on the obstacle course.

Therefore, Sam’s time will be slower than John’s.

XII. Diagramming Arguments

All the arguments we’ve dealt with – except for the last two – have been fairly simple in that the premises always provided direct support for the conclusion. But in many arguments, such as the last one, there are often arguments within arguments.

Obama example:

1. Obama couldn’t implement a single-payer healthcare system.
2. In Obama’s first term as president, both the House and Senate were under Democratic control.
3. The next president will either be dealing with the Republican controlled house and senate or at best, a split legislature.
4. Obama’s first term as president will be much easier than the next president’s term in terms of passing legislation.

∴ The next president will not be able to implement a single-payer healthcare system.

It’s clear that premises #2 and #3 are used in support of #4. And #1 in combination with #4 provides support for the conclusion.

When we diagram arguments, the aim is to represent the logical relationships between premises and conclusion. More specifically, we want to identify what each premise supports and how.

This represents that 2+3 together provide support for 4

This represents that 4+1 together provide support for 5

When we say that 2+3 together or 4+1 together support some statement, we mean that the logical support of these statements are dependent upon each other. Without the other, these statements would not provide evidence for the conclusion. In order to identify when statements are dependent upon one another, we simply underline the set that are logically dependent upon one another for their evidential support. Every argument has a single conclusion, which the premises support; therefore, every argument diagram should point to the conclusion (c).

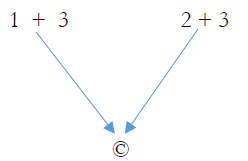
Sam Example:

1. Sam is weaker than John.
2. Sam is less flexible than John.
3. A person’s strength and flexibility inversely correlate with their time on the obstacle course.

∴ Therefore, Sam’s time will be slower than John’s.

In some cases, different sets of premises provide evidence for the conclusion independently of one another. In the argument above, there are two logically independent arguments for the conclusion that Sam’s time will be slower than John’s. That Sam is weaker than John and that being weaker correlates with a slower time provide evidence for the conclusion that Sam will be slower than John. Completely independent of this argument is the fact that Sam is less flexible and that being less flexible corresponds with a slower time. The diagram above represent these logical relations by showing that #1 and #3 dependently provide support for #4. Independent of that argument, #2 and #3 also dependently provide support for #4. Therefore, there are two logically independent sets of premises that provide support for the conclusion.

Try diagramming the following argument for yourself. The structure of the argument has been provided below:

1. All humans are mortal
2. Socrates is human
3. So Socrates is mortal.
4. If you feed a mortal person poison, he will die.

∴ Therefore, Socrates has been fed poison, so he will die.