Chapter 8 Propositional Logic, Truth Tables, and Truth Trees

wilburh

8 Chapter 8 Propositional Logic, Truth Tables, and Truth Trees

Part I: Propositional Logic (Operators and Translations)

Reasons for taking a formal approach to logic

Often, ordinary arguments in natural languages like English involve:

- ambiguity
- vagueness
- unclarity
- unstated premises
- implicit, unstated conclusions

This makes argument analysis and evaluation difficult so that it cannot be carried out in a clear, decisive way. We can avoid these problems and focus on certain important logical features of language by studying artificial, simplified languages that have none of the above features. That is the approach we will take in this section on “Truth-Functional Logic.” We will develop a simple formal language. The lessons we learn from the study of this formal language can then be applied to normal argumentation of natural language.

The symbolic language of truth-functional logic.

Vocabulary:

Logical operators (or connectives): ~, &, $\vee$ , →, $\longleftrightarrow$ .

Sentence letters: A, B, C, D …

Parentheses: ( )

Well-formed formulas (wffs):

1. Every sentence letter is a wff.

2. Suppose $\triangle$ is any wff, then ~ $\triangle$ is also a wff.

3. Suppose that $\triangle$ and $\square$ are both wffs, then so are the following:

( $\triangle$ & $\square$ )

( $\triangle$ $\vee$ $\square$ )

( $\triangle$ $\longrightarrow$ $\square$ )

( $\triangle$ $\longleftrightarrow$ $\square$ )

4. Nothing else counts as a wff.

Notes on operators

The scope of the occurrence of an operator is the smallest wff that contains that occurrence.

Example. Find the scope of each operator in the following wffs:

~(A $\longrightarrow$ ~(A $\longrightarrow$ B)) (~A $\longrightarrow$ ~(A $\longrightarrow$ B))

The main operator of a formula is the operator whose scope includes the whole formula.

Examples: Find the main operators of the following formulas:

(a) ~(A $\longrightarrow$ ~(A $\longrightarrow$ B))

(b) ~(~A $\longrightarrow$ ~(A $\longrightarrow$ B))

(c) ((A & B) $\vee$ C)

(d) (~A $\longrightarrow$ ~(A $\longrightarrow$ B))

(e) ~ ~ ~ ~B

(f) (A & (B $\vee$ C))

A negation is a wff whose main operator is a ~

A conjunction is a wff whose main operator is a &

A disjunction is a wff whose main operator is a $\vee$

A conditional is a wff whose main operator is a →

A biconditional is a wff whose main operator is a ↔

In the conditional (A $\longrightarrow$ B), A is called the antecedent and B is called the consequent.

In the conjunction (A & B), A and B are both called conjuncts.

In the disjunction (A $\vee$ B), A and B are both called disjuncts.

Semantics of the language

Roughly speaking:

“&” translates “and”

“ $\vee$ ” translates “or”

“ $\longrightarrow$ ” translates “if…then…”

“ $\longleftrightarrow$ ” translates “if and only if”

“~” translates “not”

This is only a rough translation. For example, the expression “if…then…” may have several senses, and only one will be translated by “ .” The precise meaning of the logical operators can be given by truth tables as follows, where “T” means “true” and “F” means “false.”

$\square$	~ $\square$
T	F
F	T

$\square$	$\triangle$	( $\square$ & $\triangle$ )	( $\square$ $\vee$ $\triangle$ )	( $\square$ $\longrightarrow$ $\triangle$ )	( $\square$ $\longleftrightarrow$ $\triangle$ )
T	T	T	T	T	T
T	F	F	T	F	F
F	T	F	T	T	F
F	F	F	F	T	T

A distinction is sometimes drawn between the inclusive disjunction (inclusive “or”) and the exclusive disjunction (exclusive “or”). “Either P or Q” is true on the inclusive reading of “or” just as long as at least one of P, Q is true. “Either P or Q” is true on the exclusive reading of “or” just as long as at exactly one of P, Q is true. Our default reading of “or” will be the inclusive reading. The logic symbol “” will always be understood as representing the inclusive disjunction.

Exercise 8.1: Translation into logical symbolism.

Translate the sentences below into the propositional calculus using the following key:

B: Ben likes ice cream.

J: Jerry likes ice cream.

M: Marcia likes ice cream.

Use ‘&’ to symbolize ‘and,” $\vee$ ‘ to symbolize ‘either…or…’, and ‘~’ to symbolize ‘not.’ Be sure to use parentheses so that your translations are not ambiguous. If a sentence cannot be translated because it is ambiguous, explain the ambiguity.

1. Ben likes ice cream and Jerry likes ice cream.

2. Ben and Jerry like ice cream.

3. Ben or Jerry like ice cream.

4. Ben likes ice cream and Jerry likes ice cream or Marcia likes ice cream.

[Statement 4 is ambiguous. 5-8 avoid this ambiguity.]

5. Ben and Jerry like ice cream or Marcia likes ice cream.

6. Either Ben likes ice cream and Jerry likes ice cream or Marcia likes ice cream.

7. Ben likes ice cream and either Jerry or Marcia likes ice cream.

8. Ben likes ice cream and Jerry or Marcia like ice cream.

9. Ben doesn’t like ice cream and Jerry doesn’t like ice cream.

10. It’s not the case that both Ben and Jerry like ice cream.

11. Ben and Jerry do not both like ice cream.

12. Ben and Jerry both do not like ice cream.

13. Either Ben doesn’t like ice cream or Jerry doesn’t like ice cream.

14. It is not the case that either Ben or Jerry likes ice cream.

15. Neither Ben nor Jerry likes ice cream.

Exercise 8.2: Translation into logical symbolism.

Translate the sentences below into symbolic notation using the following key:

A: There are apples in the bag.

B: There are bananas in the bag.

C: There are cookies in the bag.

D: There are doughnuts in the bag.

Use ‘&’ to symbolize ‘and’ ‘ $\vee$ ‘ to symbolize ‘either…or…’, and ‘ $\longrightarrow$ ‘ to symbolize ‘if…then…’. Be sure to use parentheses so that your translations are not ambiguous.

(1) There are apples and cookies in the bag.

(2) If there are bananas in the bag then there are cookies in the bag.

(3) If there are apples and bananas in the bag then there are cookies and doughnuts in the

bag.

(4) Either there are apples in the bag or there are cookies and doughnuts in the bag.

(5) There are apples in the bag and there are either cookies or doughnuts in the bag.

(6) Either there are apples and bananas in the bag or there are cookies and doughnuts in

the bag.

(7) If there are apples and bananas in the bag then there are either cookies or doughnuts in the bag.

Exercise 8.3: Identifying well-formed formulas.

Put an “X” next each of the following that is not a wff. For each that is a wff, circle its

main operator.

(1) ~S

(2) ~~S

(3) ~~~S

(4) (~~~S $\longrightarrow$ P)

(5) (~(P $\vee$ Q) $\longleftrightarrow$ ~~(R $\longrightarrow$ S))

(6) ~((P $\vee$ Q) $\longleftrightarrow$ ~~(R $\longrightarrow$ S))

(7) ~(~(P $\vee$ Q) ~& ~(R $\longrightarrow$ S))

(8) ((((A $\longrightarrow$ A) $\longrightarrow$ A) $\longrightarrow$ A) $\longrightarrow$ A)

(9) (A $\longrightarrow$ (A $\longrightarrow$ (A $\longrightarrow$ (A $\longrightarrow$ A))))

(10) ((((A $\longrightarrow$ A) $\longrightarrow$ A) $\longrightarrow$ A) $\longrightarrow$ A))))

(11) (P ~ Q)

(12) ((A & B) $\longrightarrow$ (B & C) $\longrightarrow$ (C & D))

Exercise 8.4

Imagine the following situation. There was a very bad leak and someone (you don’t know who) came to try to fix it. The leak wasn’t fixed unless that person succeeded in fixing it. The leak was so bad that most plumbers could not fix it, though some plumbers could. And any person who was not a plumber definitely could not fix it. From this information, which of the following conclusions can be drawn? Circle the sentences that we can conclude are true on the basis of the above information.

(1) If a plumber came, then the leak was fixed.

(2) If the leak was fixed, then a plumber came.

(3) The leak was fixed only if a plumber came.

(4) A plumber came only if the leak was fixed.

(5) The leak was fixed if a plumber came.

(6) A plumber came if the leak was fixed.

(7) The leak was fixed if, and only if, a plumber came.

(8) A plumber came if, and only if, the leak was fixed.

Now go back and symbolize the sentences, letting “P” stand for “A plumber came” and letting “L” stand for “the leak was fixed”. Only use the connectives “ $\longrightarrow$ ” and “ $\longleftrightarrow$ “.

Exercise 8.5: Translation into logical symbolism.

Translate sentences (1) through (15) below into the propositional calculus using the following key:

P: The plumber came. L: The leak has been fixed.

C: The carpenter came. G: A good job was done.

(1) Either the plumber or the carpenter came.

(2) The plumber came but the carpenter didn’t.

(3) If the plumber came then the leak was fixed, but if the carpenter came the leak was not fixed.

(4) The leak was fixed if the plumber came.

(5) The leak was fixed only if the plumber came.

(6) The leak was fixed if and only if the plumber came.

(7) A good job was done only if the plumber and the carpenter came.

(8) If the plumber came but not the carpenter, then, though the leak was fixed, a good job was not done.

(9) The plumber and the carpenter didn’t both come.

(10) Neither the plumber nor the carpenter came.

(11) Either the plumber came and the leak was fixed or the carpenter came and the leak was not fixed.

(12) Although the leak was fixed, the plumber did not come.

(13) The plumber did not come, but the carpenter came and a good job was done.

(14) Either the plumber or the carpenter came, but not both.

(15) If the leak was fixed and a good job was done, then the plumber and carpenter both came, but if either the leak was not fixed or a good job was not done, then they didn’t both come.

Part II: Fundamental concepts of truth-functional logic

A wff is a tautology provided that it is always true no matter what truth values the sentence letters may be given; i.e., it is true under every assignment of truth values to sentence letters. (Example: (P $\vee$ ~P))

A wff is a contradiction (or an inconsistency) provided that it is always false no matter what truth values the sentence letters may be given; i.e., it is false under every assignment. (Example: (P & ~P))

A wff is a contingency provided that it is true under at least one way of giving truth values to the sentence letters and it is false under at least one way of giving truth values to the sentence letters; i.e., it is true under some assignment and false under some assignment. (Example: P)

A set of wffs is truth-functionally equivalent, provided that they always have the same truth value no matter what truth values the sentence letters may have.

A set of wffs is consistent, provided that there is some way of giving truth values to the sentence letters that make all the wffs in the set true together. (Example: {(A $\vee$ B), ~A, (C & B)} is consistent because we can make all the wffs true by letting B and C be true and A be false.)

A set of wffs is inconsistent provided that it is not consistent, i.e., there is no way to give truth values to the sentence letters that make all the wffs in the set true together. (Example: {A, ~A})

An argument whose premises and conclusion are wffs is valid, provided that there is no way to give truth values to the sentence letters that make all the premises true and the conclusion false.

Truth Table Tests

Truth table test for tautology, inconsistency, or contingency

1) Construct a truth table for the wff to be tested.

2) Check the column under the main operator:

a) If it contains only T’s, the wff is a tautology.

b) If it contains only F’s, then the wff is an inconsistency (i.e., a contradiction).

c) If it contains at least one T and at least one F, then the wff is a contingency.

Truth table test for truth-functional equivalency of a pair of wffs:

1) Construct a single truth table that contains both wffs.

2) Check to see if the column of truth values under the main operator of the first wff is identical to the column of truth values under the main operator of the second wff.

a) if they are, then the pair of wffs is truth-functionally equivalent.

b) if not, then the wffs are not truth-functionally equivalent.

Truth table test for the consistency/inconsistency of a set of wffs:

1) Construct a single truth table that contains all the wffs in the set.

2) Check to see whether there is a single row of the table in which there is a T under the main operator of every wff in the set.

a) If there is the set of wffs is consistent.

b) If there is not, then the set of wffs is inconsistent.

Truth table test for validity:

1) Construct a single truth table that contains all of the premises and the conclusion.

2) Check to see whether there is a row of the table in which all the premises come out true and the conclusion is false.

a) If there is, then the argument is invalid.

b) If there is not, then the argument is valid.

Note: If the argument is invalid, then assigning truth values to the sentence letters that make the premises true and the conclusion false is called a counterexample to the validity of the argument.

Exercise 8.6: Determining truth values of sentences.

Let A, B, and C be true sentences and X, Y and Z be false sentences. Identify the truth

values of the following sentences.

1. (A $\vee$ B) & (X $\vee$ C)

2. (A & B) $\vee$ (X & C)

3. (~A $\vee$ ~B) & (~X $\vee$ ~C)

4. ~(A $\vee$ B) & (X $\vee$ C)

5. ~((A $\vee$ B) & (X $\vee$ C))

6. ~([(A & X) $\vee$ (~A & X)] & [~(A & ~(B & C)) $\vee$ (X $\vee$ (~Y & B))])

Exercise 8.7: Simple truth table exercises.

Complete the following truth tables.

1.

A

B

~

A

$\vee$

~

B

T

F

T

F

2.

A

B

~

(

A

$\vee$

~

B

)

T

F

T

F

3.

A

B

~

(

A

&

~

B

)

T

F

T

F

Exercise 8.8: Truth table test for tautology, truth-functional contingency and

inconsistency.

Complete the following truth tables and indicate whether each formula is a tautology, a truth functional contingency, or an inconsistency.

A

B

(1)

P

$\vee$

~

(Q

&

P)

T

F

T

F

(2)

(P

$\longrightarrow$

Q)

$\vee$

(Q

$\longrightarrow$

P)

P

Q

(3)

P

$\longrightarrow$

~

(Q

&

P)

T

F

T

F

(4)

~

(Q

$\longrightarrow$

P)

&

~

Q

P

Q

R

(5)

(P

$\longleftrightarrow$

Q)

$\longrightarrow$

((P

$\longrightarrow$

R))

(6)

~

(R

&

P)

$\vee$

Q

T

F

T

F

T

F

T

F

T

F

T

F

P

Q

R

(7)

(P

&

Q)

$\longrightarrow$

((P

$\vee$

R)

&

(Q

$\vee$

R))

(8)

~

((R

&

P)

$\longrightarrow$

(R

$\vee$

Q)

T

F

T

F

T

F

T

F

T

F

T

F

Exercise 8.9: Truth table test for validity.

Test the following argument for validity using the truth table method. If the argument is invalid, give a counterexample (i.e., assigning truth values to the sentence letters which makes all the premises true and the conclusion false).

Exercise 8.10: Truth table test for truth functional equivalence.

Use truth tables to test whether each of the following pairs of formulas are truth-functionally equivalent.

Q $\longrightarrow$ P

(P & Q) $\vee$ (P & R)

(P & Q) $\vee$ (P & ~Q)

(~P & ~Q)

(~P $\vee$ ~Q)

(~P & ~Q)

(~P $\vee$ ~Q)

(P & Q) $\longrightarrow$ R

~Q $\longrightarrow$ ~ P

(1) P $\vee$ ~Q

(2) P & (Q $\vee$ R)

(3) P

(4) ~(P & Q)

(5) ~(P $\vee$ Q)

(6) ~(P $\vee$ Q)

(7) ~(P & Q)

(8) P $\longrightarrow$ (Q $\longrightarrow$ R)

(9) P $\longrightarrow$ Q

PART THREE: TREE METHODS FOR TRUTH-FUNCTIONAL LOGIC I.

Tree rules: Let “O” and “ $\square$ ” stand for any formulas. Summary of tree rules:

Tree rule details: Once a rule has been applied to a line, check off the line (X). Only apply rules to unchecked whole lines.

If a path through a tree has a wff $\square$ as one line and a wff ~ $\square$ as another line, then close off that path by putting an “X” at the bottom of the path. A path that does not have a wff and its negation as whole lines is called an open path. A closed path is any path that contains a wff and its negation as separate lines.

& rule: If an open path contains a wff of the form (O & ) as a whole line then at the bottom of each open path that contains that line add the lines O and $\square$ .

~& rule: If an open path contains a wff of the form ~(O & ) as a whole line then at the bottom of each open path that contains that line add a pair of branches to the path: on one of the branches write ~O and on the other branch write ~ $\square$ .

$\vee$ rule: If an open path contains a wff of the form (O $\vee$ ) as a whole line then at the bottom of each open path that contains that line add a pair of branches to the path: on one of the branches write O and on the other branch write $\vee$ .

~ $\vee$ rule: If an open path contains a wff of the form ~(O $\vee$ ) as a whole line then at the bottom of each open path that contains that line add the lines ~O and ~ $\vee$ .

$\longleftrightarrow$ rule: If an open path contains a wff of the form (O $\longleftrightarrow$ $\square$ ) as a whole line then at the bottom of each open path that contains that line add a pair of branches to the path: on one of the branches add the lines  and , and on the other branch add the lines ~O and ~ $\square$ .

~ $\longleftrightarrow$ rule: If an open path contains a wff of the form ~(O $\longleftrightarrow$ ) as a whole line then at the bottom of each open path that contains that line add a pair of branches to the path: on one of the branches add the lines O and ~ $\square$ , and on the other branch add the lines ~O and $\square$ .

$\longrightarrow$ rule: If an open path contains a wff of the form (O $\longrightarrow$ $\square$ ) as a whole line then at the bottom of each open path that contains that line add a pair of branches to the path: on one of the branches write ~O and on the other branch write $\square$ .

~ $\longrightarrow$ rule: If an open path contains a wff of the form ~(O $\longrightarrow$ $\square$ ) as a whole line then at the bottom of each open path that contains that line add the lines O and ~ $\square$ .

~~ rule: If an open path contains a wff of the form ~~ $\square$ as a whole line then at the bottom of each open path that contains that line add the line $\square$ .

II. Tree test for consistency of a set of wffs.

1. Begin a tree by listing the wffs to be tested.

2. Construct the tree.

3. Does the tree have an open path?

Yes. Then the set is consistent.

No. Then the set is inconsistent.

Note that if there is an open path, then a verifying assignment for the set of wffs can be found. A verifying assignment for a set of wffs is an assignment of truth values to sentence letters that makes all the sentences in the set true together. To find a verifying assignment, first choose any open path. If a sentence letter appears as a whole line on that path, then assign TRUE to that letter. If the negation of a sentence letter appears as a whole line on the path, assign FALSE to the sentence letter. If neither the sentence letter nor its negation appears as a whole line on the path, it may be assigned either TRUE or FALSE.

III. Tree test to determine whether a wff, O, is a tautology, a truth-functional contingency, or an inconsistency.

1. Construct two trees, one for O and one for ~O.

2. Does the tree for O completely close? If it does then O is inconsistent.

3. Does the tree for ~O completely close? If it does then O is a tautology.

4. Do both of the trees each have an open path? If they do then O is a truth-functional contingency.

IV. Tree test for validity of an argument.

1. Begin a tree by listing all the premises of the argument as well as the negation of the conclusion.

2. Construct the tree.

3. Does the tree have an open path?

Yes. Then the argument is invalid.

No. Then the argument is valid.

If the argument is invalid, a counterexample can be read off any open path. A counterexample is a truth value assignment that makes the premises true and the conclusion false. To obtain the counterexample use the method for reading an assignment off an open path that was set out above with the test for consistency.

V. Tree test for truth-functional equivalence of O and O.

1. Construct a tree for the wff ~(O $\longleftrightarrow$ $\square$ )

2. Do all the paths close?

Yes. Then O and $\square$ are truth-functionally equivalent.

No. Then O and $\square$ are not truth-functionally equivalent.

Note: the reason this test works is that O and $\square$ are equivalent if and only if ~(O $\longleftrightarrow$ $\square$ ) is a

VI. Warnings and hints.

1. Only close off a path if a formula and its negation appear as whole lines on the path. So, for example, if ~P occurs as a complete line on a path and P occurs earlier as a whole line on that path, then you should close the path. On the other hand, if ~P occurs on a path and above it on the path the formula (P $\longrightarrow$ Q) occurs, that does not give you any reason to close off the path.

2. When you apply a rule to a particular line on a path, write the results just at the bottom of all the open paths that contain the line in question.

3. You can apply the rules in any order you wish, but you can often save time and space by applying the non-branching rules first.

4. Apply the rules to whole lines only, never to mere parts of a line.

PART THREE EXERCISES

Exercise 8.11: Warm up exercises.

Imitate the following example to answer the subsequent problems.

Example: Determine whether the statements on the left are consistent with each other?

Either Bill, Jim and Mike ate, or Dave, Patty and Robert ate.

Either Bill or Robert didn’t eat.

Jim didn’t eat and Mike didn’t eat.

Are the following sets of statements consistent? Solve using the same method. If they are consistent, provide all the verifying assignments.

1. Either Bill and Jim ate, or Mike and Dave ate.

Either Jim didn’t eat or Mike didn’t eat.

2. Either Bill and Jim ate, or Mike and Dave ate.

Jim didn’t eat and Mike didn’t eat.

3. Either Bill and Jim ate, but not Mike, or Dave and Patty ate, but not Robert. Bill didn’t eat and neither did Robert.

Jim ate and so did Patty and Mike

Exercise 8.12: Tree test for consistency using &, 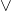$\vee$ and ~.

Use the tree method to test the following sets of wffs for consistency. Indicate whether each set of wffs is consistent or inconsistent. If it is consistent, provide a verifying assignment (i.e., an assignment of truth values to the sentence letters which makes all the sentences in the set true together).

Exercise 8.13: Tree test for consistency.

Same instructions as for Part Two.

Exercise 8.14: Tree test for tautology, inconsistency, and truth functional contingency.

Use the tree method to determine whether each of the following is a tautology, inconsistency or truth functionally contingent.

Exercise 8.15: Tree test for validity.

Use the tree method to test the following arguments for validity. If an argument is invalid provide a counterexample.

Exercise 8.16: Tree test for truth-functional equivalence.

Use the tree method to do test the following pairs of wffs for truth-functional equivalence.

8 Chapter 8 Propositional Logic, Truth Tables, and Truth Trees

Part I: Propositional Logic (Operators and Translations)

Reasons for taking a formal approach to logic

The symbolic language of truth-functional logic.

Notes on operators

Semantics of the language

Exercise 8.1: Translation into logical symbolism.

Exercise 8.2: Translation into logical symbolism.

Exercise 8.3: Identifying well-formed formulas.

Exercise 8.4

Exercise 8.5: Translation into logical symbolism.

Part II: Fundamental concepts of truth-functional logic

Truth Table Tests

Exercise 8.6: Determining truth values of sentences.

Exercise 8.7: Simple truth table exercises.

Exercise 8.8: Truth table test for tautology, truth-functional contingency and

inconsistency.

Exercise 8.9: Truth table test for validity.

Exercise 8.10: Truth table test for truth functional equivalence.

PART THREE: TREE METHODS FOR TRUTH-FUNCTIONAL LOGIC I.

PART THREE EXERCISES

Exercise 8.11: Warm up exercises.

Exercise 8.12: Tree test for consistency using &, $\vee$ and ~.

Exercise 8.13: Tree test for consistency.

Exercise 8.14: Tree test for tautology, inconsistency, and truth functional contingency.

Exercise 8.15: Tree test for validity.

Exercise 8.16: Tree test for truth-functional equivalence.

License

Share This Book

Part I: Propositional Logic (Operators and Translations)

Reasons for taking a formal approach to logic

The symbolic language of truth-functional logic.

Notes on operators

Semantics of the language

Exercise 8.1: Translation into logical symbolism.

Exercise 8.2: Translation into logical symbolism.

Exercise 8.3: Identifying well-formed formulas.

Exercise 8.4

Exercise 8.5: Translation into logical symbolism.

Part II: Fundamental concepts of truth-functional logic

Truth Table Tests

Exercise 8.6: Determining truth values of sentences.

Exercise 8.7: Simple truth table exercises.

Exercise 8.8: Truth table test for tautology, truth-functional contingency and

inconsistency.

Exercise 8.9: Truth table test for validity.

Exercise 8.10: Truth table test for truth functional equivalence.

PART THREE: TREE METHODS FOR TRUTH-FUNCTIONAL LOGIC I.

PART THREE EXERCISES

Exercise 8.11: Warm up exercises.

Exercise 8.12: Tree test for consistency using &, and ~.

Exercise 8.13: Tree test for consistency.

Exercise 8.14: Tree test for tautology, inconsistency, and truth functional contingency.

Exercise 8.15: Tree test for validity.

Exercise 8.16: Tree test for truth-functional equivalence.

License

Share This Book

Exercise 8.12: Tree test for consistency using &, $\vee$ and ~.